[智能风控]如何进行模型筛选?
- 1 minKS值和KS曲线
KS(Kolmogorov-Smirnov)统计量由两位苏联数学家A.N. Kolmogorov和N.V. Smirnov提出。在风控中,KS常用于评估模型区分度。区分度越大,说明模型的风险排序能力(ranking ability)越强。
KS曲线是两条线,其横轴是阈值,纵轴是TPR与FPR。两条曲线之间之间相距最远的地方对应的阈值,就是最能划分模型的阈值。
KS值是MAX(TPR - FPR),即两曲线相距最远的距离。
什么是区分度
如果这两个分布的重叠部分越小,代表正负样本的差异性越大,自变量就能把正负样本更好地区分开。
打个比方,想象这个变量就是一双手,把这两个分布往两边拉开。这双手的力量越大,两个概率分布间隔就越远,说明变量区分性就越好。
KS值的计算过程
KS值的值域[0,1]。直观理解为 真阳率(TPR)-假阳率(FPR)。
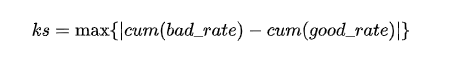
- step 1. 对变量进行分箱(binning),可以选择等频、等距,或者自定义距离。
- step 2. 计算每个分箱区间的好账户数(goods)和坏账户数(bads)。
- step 3. 计算每个分箱区间的累计好账户数占总好账户数比率(cum_good_rate)和累计坏账户数占总坏账户数比率(cum_bad_rate)。
- step 4. 计算每个分箱区间累计坏账户占比与累计好账户占比差的绝对值,得到KS曲线。
- step 5. 在这些绝对值中取最大值,得到此变量最终的KS值
KS反应的模型含义
好坏样本累计差异越大,KS指标越大,那么模型的风险区分能力越强。
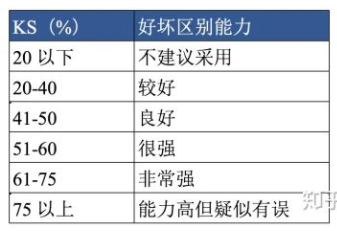
KS与其他评估指标的区别
为什么风控选用KS值作为评估模型的标准?
风控建模时,我们常把样本标签分为GBIX四类,其中:G = Good(好人,标记为0),B = Bad(坏人,标记为1),I = Indeterminate (不定,未进入表现期),X = Exclusion(排斥,异常样本)。
需要指出的是,Good和Bad之间的定义往往是模糊、连续的,依赖于实际业务需求
🌟例1:模糊性
对于12期信贷产品,如果设定表现期为前6期,S6D15(前6期中任意一期逾期超过15天)就是1,否则为0;但是后来如果把表现期调整为前3期,那么对于“前3期都正常还款,但4~6期才发生逾期并超过15天“的这部分样本而言,原本所定义的label就从1就变成0了。 因此,业务需求的不同,导致标签定义不是绝对的。
🌟例2:连续性
定义首期逾期超过30天为1,否则为0。但是,逾期29天和逾期31天的用户之间其实并没有不可跨越的硬间隔,逾期29天的用户可能会进一步恶化为逾期31天。 由于逾期的严重程度定义本身就带有一定的主观性,我们很难说逾期天数差几天有多少本质的差异,所以哪怕我们为了转化为分类问题做了硬性的1和0的界限定义,但在业务上理解还是一个连续问题。
因此在风控中,y的定义并不是非黑即白(离散型),而用概率分布(连续型)来衡量或许更合理。
我们通常用概率分布来描述这种模糊的软间隔概念,也倾向于使用LR这种概率模型,而不是SVM这种以边界距离作为优化目标的模型。
那为什么选择KS指标呢?——KS指标倾向于从概率角度衡量正负样本分布之间的差异。正是因为正负样本之间的模糊性和连续性,所以KS也是一条连续曲线。但最终为什么取一个最大值,主要原因是提取KS曲线中的一个显著特征,从而便于相互比较。
几何角度解释KS与ROC的关系
ROC曲线的横轴是FPR,纵轴是TPR。我们计算的时候希望AUC越大越好。这样模型的分类效果好。
希望TPR尽可能高,FPR尽可能低,我们可以设计一个目标函数就是KS值。
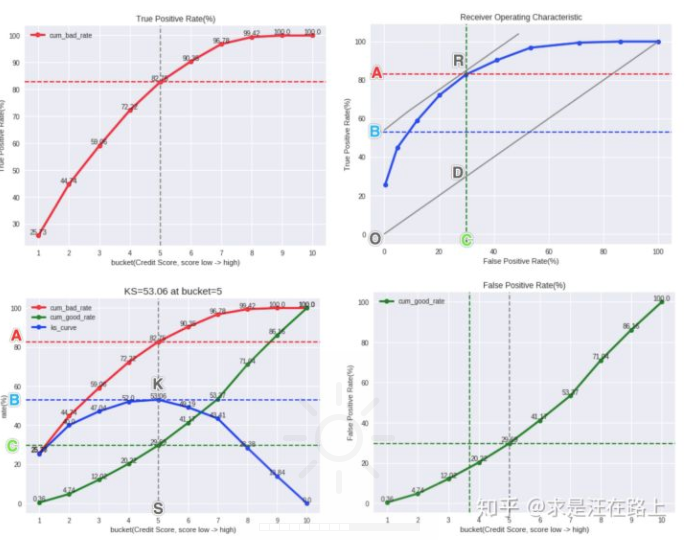
以UCI Credit的数据为例,以xgb作为模型画KS曲线。先看表格
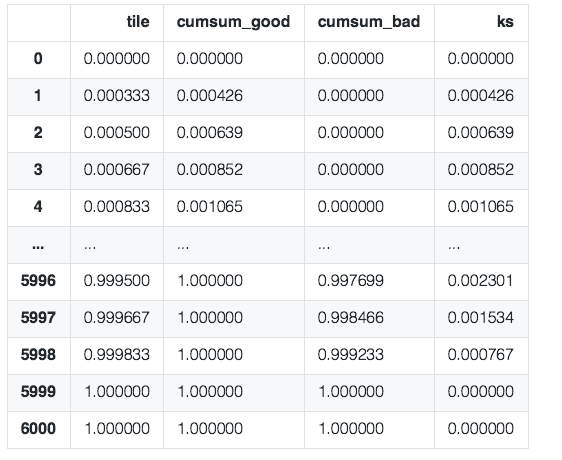
其曲线为
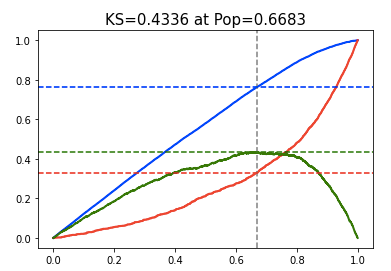
参考知乎上的图:
- 辅助曲线:TPR(图左上)、FPR(图右下)。
- 辅助直线:红线为取得max_ks时的cum_bad_rate,绿线为取得max_ks时的cum_good_rate,蓝线为max_ks。灰线BR为ROC曲线在R点的切线,且与对角线OD平行。
| 为什么要在R点加上一条切线?🤔这是因为$KS = | TPR - FPR | $,如果添加辅助线$TPR = FPR + KS$,那么这条直线的截距就是KS值。当与ROC曲线相切时,截距最大,也就对应max_ks。 |
若希望KS尽可能大,那么R需要尽可能接近(0,1),此时AUC一般也会增大。 对于相同的KS值,在KS曲线上有两个选择,但TPR和FPR同时大或同时小。虽然我们的目的通常是抓对更多的坏人(TPR⬆),尽可能减少错抓的好人(FPR⬇),但两者需要trade-off。到底选择哪个阈值,取决于业务目标:是希望对bad有更高的召回,还是对good有更低的误伤? 由于KS只是在一个最大分隔点时的值,并不够全面。通常我们也会同时参考KS和AUC(或Gini)
左上—TPR,右上—ROC,左下—KS,右下—FPR
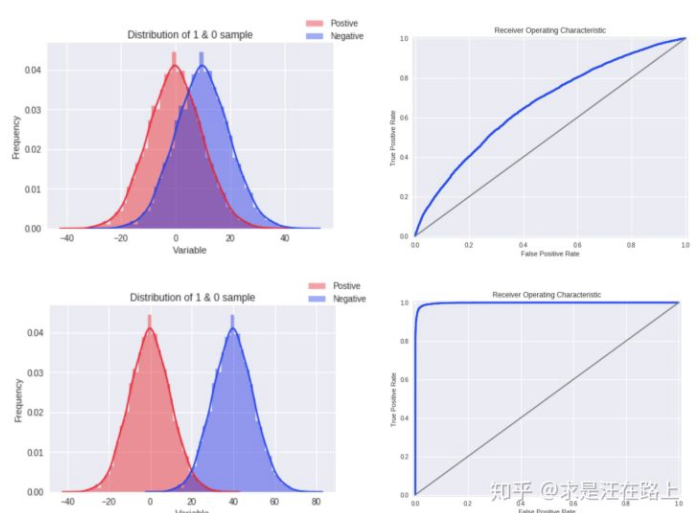
如果KS达到80%以上,此时ROC曲线就会变得很畸形。为了便于制定策略,模型评分在放贷样本上一般要求服从正态分布。如果出现这种明显的双峰分布,就不太符合业务sense
参考资料: