[智能风控]金融风控专题浅谈

Monday. April 06, 2020 - 1 min

金融风控专题浅谈与规则挖掘

前言

时隔两年，重新开始博客，两年时间偶尔也记录一些技术内容，但是怠慢着就没有系统发出来。从去年毕业入职，在金融风控方面也算是入行了一年多的时间。时常觉得，想做的事情、相了解的东西太多，时间就匆匆。前几天旧友小聚，在钱塘江畔，看到满满的人间烟火气，想想这一年，一直在犹豫、徘徊和不知所措中度过。

经过这次疫情，想想人生无常，苦多乐少，有很多事情记得不如忘了。

新开一个金融风控专题，算是记录自己的日常学习与生活。

金融风控建模浅谈

任何的风控建模离不开三个因素：数据信息、策略体系和模型。

数据信息对应很多方面：内部的数据挖掘（用户基本信息、用户行为数据、用户授信、用户关联网络等）

策略体系：反欺诈规则、准入规则、风险预警、网贷规则等

模型：模型主要是对应业务任务的，toC和toB都需要风险管控，供应链金融和消费者金融的风控有区别又相互联系，但是离不开欺诈检测、风险评级、风险定价、流失预警、授信等。金融风控的模型大部分属于二分类任务，看起来很简单，但实际上要对业务深入挖掘，同时还有一些图模型和聚类模型也适合金融欺诈任务。

完整的工业建模流程：

将业务定义为抽象的分类或者回归问题
标签定义与提取
样本选取，构建数据集
特征工程+模型训练+模型评价+模型调优
输出模型报告
上线与监控+验证与迭代

每个环节都有一些坑需要我们去添补，我讲一下我遇到的几个问题。

数据环节

标签不完全可信
- 最方便的是业务能够给你的可信的标签，这样数据的稳定性是最高的。但是有时候，要考虑当标签不完全可信的时候，如何操作来保证模型尽可能有效？
灰样本定义
- 正负样本间存在大量灰色样本，如逾期3-15天的人，以后可能是高风险人群，也有可能之后没有风险，而他们的个体差异可能非常大，加入模型训练后不利于划分出清晰的类间距。
正负样本不均横
- 常见方法是对正样本欠采样，当然我们也可以对负样本进行过采样,或者采用一些模型方法，smote等生成样本。
时间窗口
- 金融风控的大部分任务依赖于时间窗口，一个用户的信息可以分为观察期和表现期。观察期在于业务事件（个人借贷、股票买入卖出、信贷申请等）发生前。表现期是定义标签的时间区域，一般位于观察期的观测点之后（是否逾期，是否违约，净值波动程度等）。
- 故金融数据划分实际上金融序列的划分。分为开发样本，验证样本和时间外样本（OOT）。

模型与评估

金融领域的任务有一个特点就是需要强可解释性。具几个例子，比如C端消费者，你把他定位为黑户了或者他的蚂蚁分非常低，你不能就说这是神经网络学习出来的，很难解释，这我要是消费者我肯定要一个合理的解答。同样，B端业务银行信贷或者基金、QD风控，业务需要满足银监会或者证监会的标准，需要进行合理的解释。所以可解释性可能是不同于CV或者一般NLP任务的点。具体的模型后面我也边学习边记录吧。

上线评估。标准的评估有一个标准。

测试集按照评分升序排序
分箱
分箱后计算指标（KS值、负样本个数、捕获率、负样本占比等）

学习笔记-规则挖掘01

这一部分代码在学习的时候手码了一遍，大体流程总结一下，主要是利用基本的统计特征，然后cast回归树计算每次分裂的特征从而生成有效的业务规则，这种直接的业务规则可以相对直接的减少风险，高可解释性，但是准确度差一点。

数据特征工程阶段划分为三个部分。

标签
离散特征
连续特征

对于连续值可以进行特征衍生，统计特征（最小值、最大值、方差、极差、变异系数等）每个统计特征的意义不一一解释了。这里主要用groupby之后apply做一些函数进去，这里学到了如何用np.nanxx进行聚合，之前都是先去掉空值再做。离散特征的衍生可以进行计数、交叉或者组合特征。这里知识点比较多，后面遇到合适的项目再慢慢补。

最后merge一下做好的dataframe，然后放进cart回归树。这里回归树的参数在生成业务规则时一般不用太深的树，同时控制最小叶子样本数和分裂样本数，防止过拟合。最后画出图像，生成业务规则。

实现代码

   
  import pandas as pd
import numpy as np
import os
print(os.getcwd())
data = pd.read_excel('In_risk/data_for_tree.xlsx')
data.head()
#%%

org_lst = ['uid','create_dt','oil_actv_dt','class_new','bad_ind']
#agg_lst离散型变量 dstc_lst 连续性变量
agg_lst = ['oil_amount','discount_amount','sale_amount','amount',\
           'pay_amount','coupon_amount','payment_coupon_amount']
dstc_lst = ['channel_code','oil_code','scene','source_app','call_source']

df = data[org_lst].copy()
df[agg_lst] = data[agg_lst].copy()
df[dstc_lst] = data[dstc_lst].copy()
#丢弃第一次出现的重复行，
base = df[org_lst].copy()
base = base.drop_duplicates(['uid'],keep='first')
def combine(gn,tp):
    if gn.empty==True:
        gn = tp
    else:
        gn = pd.merge(gn,tp,on='uid',how='left')
    del tp
    return gn

gn = pd.DataFrame()
for i in agg_lst:
    #计算个数
    tp = pd.DataFrame(df.groupby('uid').apply(
        lambda df:len(df[i])).reset_index())
    tp.columns = ['uid',i+'_cnt']
    gn = combine(gn,tp)
    
    #计算历史特征值大于0的个数
    tp = pd.DataFrame(df.groupby('uid').apply(
        lambda df:np.where(df[i]>0,1,0).sum()).reset_index())
    tp.columns = ['uid',i+'_num']
    gn = combine(gn,tp)
    
    #求和历史数据
    tp = pd.DataFrame(df.groupby('uid').apply(
        lambda df:np.nansum(df[i])).reset_index())
    tp.columns = ['uid',i+'_tot']
    gn = combine(gn,tp)
    
    #历史数据求平均值
    tp = pd.DataFrame(df.groupby('uid').apply(
        lambda df:np.nanmean(df[i])).reset_index())
    tp.columns = ['uid',i+'_avg']
    gn = combine(gn,tp)

    #对历史数据求最大值
    tp = pd.DataFrame(df.groupby('uid').apply(
        lambda df:np.nanmax(df[i])).reset_index())
    tp.columns = ['uid',i+'_max']
    gn = combine(gn,tp)

    #对历史数据求最小值
    tp = pd.DataFrame(df.groupby('uid').apply(
        lambda df:np.nanmin(df[i])).reset_index())
    tp.columns = ['uid',i+'_min']
    gn = combine(gn,tp)
    
    #对历史数据求方差
    tp = pd.DataFrame(df.groupby('uid').apply(
        lambda df:np.nanvar(df[i])).reset_index())
    tp.columns = ['uid',i+'_var']
    gn = combine(gn,tp)
    
    #对历史数据求极差
    tp = pd.DataFrame(df.groupby('uid').apply(
        lambda df:np.nanmax(df[i])- np.nanmin(df[i])).reset_index())
    tp.columns = ['uid',i+'_ran']
    gn = combine(gn,tp)
    
    #对历史数据求变异系数
    tp = pd.DataFrame(df.groupby('uid').apply(
        lambda df:np.nanmean(df[i])/(np.nanvar(df[i])+0.01)).reset_index())
    tp.columns = ['uid',i+'_cva']
    gn = combine(gn,tp)
#%%
#离散变量的特征衍生
gc = pd.DataFrame()
for i in dstc_lst:
    tp = pd.DataFrame(df.groupby('uid').apply(
        lambda df:len(set(df[i]))).reset_index())
    tp.columns = ['uid',i+'_dstc']
    gc = combine(gc,tp)
    fn = base.merge(gn,on='uid')
fn = pd.merge(fn,gc,on='uid')
fn.shape

fn = fn.fillna(0)
from sklearn import tree
x = fn.drop(['uid','oil_actv_dt','create_dt','bad_ind','class_new'],axis=1)
y = fn.bad_ind.copy()

dtree = tree.DecisionTreeRegressor(
    max_depth = 2,
    min_samples_leaf = 500,
    min_samples_split = 5000
)
dtree = dtree.fit(x,y)

import pydotplus
from IPython.display import Image
from sklearn.externals.six import StringIO
import os

dot_data = StringIO()
tree.export_graphviz(dtree, 
                    out_file = dot_data,
                    feature_names = x.columns,
                    class_names = ['bad_ind'],
                    filled = True,
                    rounded = True,
                    special_characters = True)
graph = pydotplus.graph_from_dot_data(dot_data.getvalue())
Image(graph.create_png())

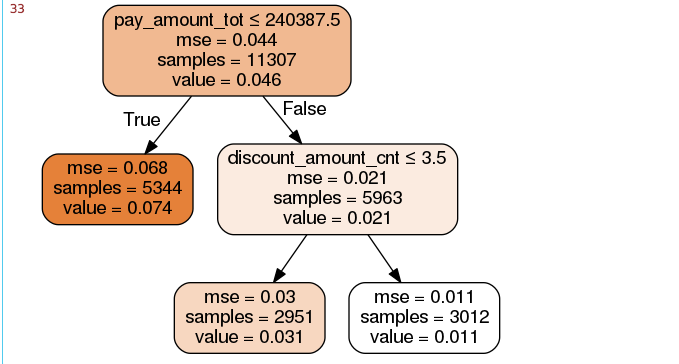
gRalh1TeOk2JVyz

在这个图中可以直接看到每一个阶段的负样本占比，mse是均方误差，value计算的是叶节点中的正负样本标签的均值。二分类下，这种计算和标签为1的样本在总样本是等价的。所以等价于逾期率。这样就可以制定三种业务规则。

参考资料：[1]: 智能风控：原理、算法与工程实践

[智能风控]金融风控专题浅谈

金融风控专题浅谈与规则挖掘

前言

金融风控建模浅谈

学习笔记-规则挖掘01

Related Posts