[智能风控]集成模型评分卡01

- 6 mins
智能风控

UCI credit 数据集

数据集的简要说明

此数据集包含有关2005年4月至2005年9月台湾地区信用卡客户的默认付款，人口统计因素，信用数据，付款历史和账单的信息。

特征列：

数据探索与划分

数据有30000行，25列，可以看到是一个不平衡的数据集。

pdy6MYJZvoE1iVG

#%%
from sklearn.model_selection import train_test_split,GridSearchCV
from sklearn.preprocessing import StandardScaler  # 数据规范化
from sklearn.pipeline import Pipeline      # 管道机制
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from IPython.display import display
#%%
import os

#%%
#数据加载
data = pd.read_csv('UCI_Credit_Card.csv')
data.head()

#%%
# 探索数据
print(data.shape) # 查看数据集大小，30000行数据，有25列
print('-'*100)
#print(data.describe())
print(data.info())

#%%
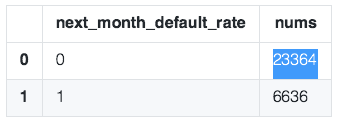
# 查看下一个月违约率的情况 1：违约，0：守约
next_month = data['target'].value_counts()
print(next_month)
# 违约情况可视化
df = pd.DataFrame({'next_month_default_rate':next_month.index,'nums':next_month.values})
df
#%%
# plt.rcParams['font.sans-serif'] = ['SimHei']
plt.figure(figsize = (3,3))
plt.title('credit card default(default:1,keeping:0)')
sns.barplot(x = 'next_month_default_rate',y = 'nums',data = df)
# 设置颜色
sns.set_color_codes('pastel')
plt.show()

数据分箱

1.分箱的好处

为什么要做特征分箱(特征离散化)？

  1. 离散特征的增加和减少都很容易，易于模型的快速迭代；
  2. 稀疏向量内积乘法运算速度快，计算结果方便存储，容易扩展；
  3. 离散化后的特征对异常数据有很强的鲁棒性：比如一个特征是年龄>30是1，否则0。如果特征没有离散化，一个异常数据“年龄300岁”会给模型造成很大的干扰；
  4. 当我们使用逻辑回归的时候，逻辑回归属于广义线性模型，表达能力受限；单变量离散化为N个后，每个变量有单独的权重，相当于为模型引入了非线性，能够提升模型表达能力，加大拟合；
  5. 离散化后可以进行特征交叉，由M+N个变量变为M*N个变量，进一步引入非线性，提升表达能力；
  6. 特征离散化以后，起到了简化了模型的作用，降低了模型过拟合的风险。 可以将缺失作为独立的一类带入模型。
  7. 变化特征尺度，所有变量变换到相似的尺度上。

如何做分箱？

以UCI的age字段做一个简单的分箱，可以看出每种分箱的差异。

2.等频分箱

区间的边界值要经过选择,使得每个区间包含大致相等的实例数量。比如说 N=10 ,每个区间应该包含大约10%的实例。

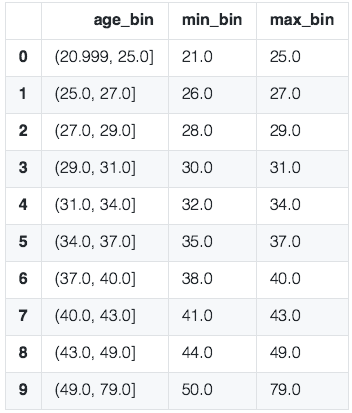
3on8Hbq7JvgISzB

#####################等频分箱#################################################
train["age_bin"] = pd.qcut(train["AGE"],10)
group_by_age_bin = train.groupby(["age_bin"],as_index=True)

df_min_max_bin = pd.DataFrame()#用来记录每个箱体的最大最小值
df_min_max_bin["min_bin"] = group_by_age_bin.AGE.min()
df_min_max_bin["max_bin"] = group_by_age_bin.AGE.max()

df_min_max_bin.reset_index(inplace=True)
df_min_max_bin

3.等距分箱

从最小值到最大值之间,均分为 N 等份。 如果 A,B 为最小最大值, 则每个区间的长度为 W=(B−A)/N , 则区间边界值为A+W,A+2W,….A+(N−1)W 。这里只考虑边界，每个等份的实例数量可能不等。

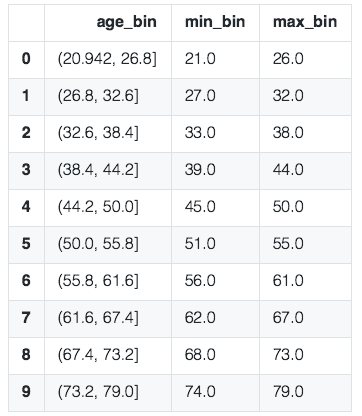
DMS1dkCQp8wBaTL

#####################等宽分箱###################################################
train["age_bin"] = pd.cut(train["AGE"],10)
group_by_age_bin = train.groupby(["age_bin"],as_index=True)

df_min_max_bin = pd.DataFrame()#用来记录每个箱体的最大最小值
df_min_max_bin["min_bin"] = group_by_age_bin.AGE.min()
df_min_max_bin["max_bin"] = group_by_age_bin.AGE.max()

df_min_max_bin.reset_index(inplace=True)
df_min_max_bin

4.卡方分箱

卡方分箱是自底向上的(即基于合并的)数据离散化方法。它依赖于卡方检验:具有最小卡方值的相邻区间合并在一起,直到满足确定的停止准则。卡方分箱是有监督的。

基本思想:对于精确的离散化，相对类频率在一个区间内应当完全一致。因此,如果两个相邻的区间具有非常类似的类分布，则这两个区间可以合并；否则，它们应当保持分开。而低卡方值表明它们具有相似的类分布。

AZET6soU4f3KxdQ

卡方阈值的确定：

阈值的意义

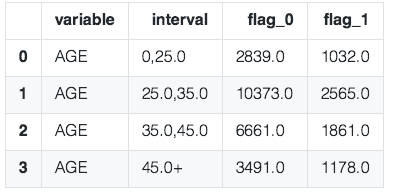
GioeKdmLI1CX39N

卡方分箱
  
  # -*- coding: utf-8 -*-
def ChiMerge(df,variable,flag,confidenceVal=3.841,bin=10,sample=None):  
    '''
    param df:DataFrame| 必须包含标签列
    param variable:str| 需要卡方分箱的变量名称（字符串）
    param flag:str    | 正负样本标识的名称（字符串）
    param confidenceVal:float| 置信度水平（默认是不进行抽样95%）
    param bin：int            | 最多箱的数目
    param sample: int          | 为抽样的数目（默认是不进行抽样），因为如果观测值过多运行会较慢
    note: 停止条件为大于置信水平且小于bin的数目
    return :DataFrame|采样结果
    '''    
    import pandas as pd
    import numpy as np
    
    
    #进行是否抽样操作
    if sample != None:
        df = df.sample(n=sample)
    else:
        df   
        
    #进行数据格式化录入
    total_num = df.groupby([variable])[flag].count()  #统计需分箱变量每个值数目
    total_num = pd.DataFrame({'total_num': total_num})  #创建一个数据框保存之前的结果
    positive_class = df.groupby([variable])[flag].sum()  #统计需分箱变量每个值正样本数
    positive_class = pd.DataFrame({'positive_class': positive_class})  #创建一个数据框保存之前的结果
    regroup = pd.merge(total_num, positive_class, left_index=True, right_index=True,
                       how='inner')  # 组合total_num与positive_class
    regroup.reset_index(inplace=True)
    regroup['negative_class'] = regroup['total_num'] - regroup['positive_class']  #统计需分箱变量每个值负样本数
    regroup = regroup.drop('total_num', axis=1)
    np_regroup = np.array(regroup)  #把数据框转化为numpy（提高运行效率）
    #print('已完成数据读入,正在计算数据初处理')

    #处理连续没有正样本或负样本的区间，并进行区间的合并（以免卡方值计算报错）
    i = 0
    while (i <= np_regroup.shape[0] - 2):
        if ((np_regroup[i, 1] == 0 and np_regroup[i + 1, 1] == 0) or ( np_regroup[i, 2] == 0 and np_regroup[i + 1, 2] == 0)):
            np_regroup[i, 1] = np_regroup[i, 1] + np_regroup[i + 1, 1]  # 正样本
            np_regroup[i, 2] = np_regroup[i, 2] + np_regroup[i + 1, 2]  # 负样本
            np_regroup[i, 0] = np_regroup[i + 1, 0]
            np_regroup = np.delete(np_regroup, i + 1, 0)
            i = i - 1
        i = i + 1
 
    #对相邻两个区间进行卡方值计算
    chi_table = np.array([])  # 创建一个数组保存相邻两个区间的卡方值
    for i in np.arange(np_regroup.shape[0] - 1):
        chi = (np_regroup[i, 1] * np_regroup[i + 1, 2] - np_regroup[i, 2] * np_regroup[i + 1, 1]) ** 2 \
          * (np_regroup[i, 1] + np_regroup[i, 2] + np_regroup[i + 1, 1] + np_regroup[i + 1, 2]) / \
          ((np_regroup[i, 1] + np_regroup[i, 2]) * (np_regroup[i + 1, 1] + np_regroup[i + 1, 2]) * (
          np_regroup[i, 1] + np_regroup[i + 1, 1]) * (np_regroup[i, 2] + np_regroup[i + 1, 2]))
        chi_table = np.append(chi_table, chi)
    #print('已完成数据初处理，正在进行卡方分箱核心操作')

    #把卡方值最小的两个区间进行合并（卡方分箱核心）
    while (1):
        if (len(chi_table) <= (bin - 1) and min(chi_table) >= confidenceVal):
            break
        chi_min_index = np.argwhere(chi_table == min(chi_table))[0]  # 找出卡方值最小的位置索引
        np_regroup[chi_min_index, 1] = np_regroup[chi_min_index, 1] + np_regroup[chi_min_index + 1, 1]
        np_regroup[chi_min_index, 2] = np_regroup[chi_min_index, 2] + np_regroup[chi_min_index + 1, 2]
        np_regroup[chi_min_index, 0] = np_regroup[chi_min_index + 1, 0]
        np_regroup = np.delete(np_regroup, chi_min_index + 1, 0)

        if (chi_min_index == np_regroup.shape[0] - 1):  # 最小值试最后两个区间的时候
            # 计算合并后当前区间与前一个区间的卡方值并替换
            chi_table[chi_min_index - 1] = (np_regroup[chi_min_index - 1, 1] * np_regroup[chi_min_index, 2] - np_regroup[chi_min_index - 1, 2] * np_regroup[chi_min_index, 1]) ** 2 \
                                           * (np_regroup[chi_min_index - 1, 1] + np_regroup[chi_min_index - 1, 2] + np_regroup[chi_min_index, 1] + np_regroup[chi_min_index, 2]) / \
                                       ((np_regroup[chi_min_index - 1, 1] + np_regroup[chi_min_index - 1, 2]) * (np_regroup[chi_min_index, 1] + np_regroup[chi_min_index, 2]) * (np_regroup[chi_min_index - 1, 1] + np_regroup[chi_min_index, 1]) * (np_regroup[chi_min_index - 1, 2] + np_regroup[chi_min_index, 2]))
            # 删除替换前的卡方值
            chi_table = np.delete(chi_table, chi_min_index, axis=0)

        else:
            # 计算合并后当前区间与前一个区间的卡方值并替换
            chi_table[chi_min_index - 1] = (np_regroup[chi_min_index - 1, 1] * np_regroup[chi_min_index, 2] - np_regroup[chi_min_index - 1, 2] * np_regroup[chi_min_index, 1]) ** 2 \
                                       * (np_regroup[chi_min_index - 1, 1] + np_regroup[chi_min_index - 1, 2] + np_regroup[chi_min_index, 1] + np_regroup[chi_min_index, 2]) / \
                                       ((np_regroup[chi_min_index - 1, 1] + np_regroup[chi_min_index - 1, 2]) * (np_regroup[chi_min_index, 1] + np_regroup[chi_min_index, 2]) * (np_regroup[chi_min_index - 1, 1] + np_regroup[chi_min_index, 1]) * (np_regroup[chi_min_index - 1, 2] + np_regroup[chi_min_index, 2]))
            # 计算合并后当前区间与后一个区间的卡方值并替换
            chi_table[chi_min_index] = (np_regroup[chi_min_index, 1] * np_regroup[chi_min_index + 1, 2] - np_regroup[chi_min_index, 2] * np_regroup[chi_min_index + 1, 1]) ** 2 \
                                       * (np_regroup[chi_min_index, 1] + np_regroup[chi_min_index, 2] + np_regroup[chi_min_index + 1, 1] + np_regroup[chi_min_index + 1, 2]) / \
                                   ((np_regroup[chi_min_index, 1] + np_regroup[chi_min_index, 2]) * (np_regroup[chi_min_index + 1, 1] + np_regroup[chi_min_index + 1, 2]) * (np_regroup[chi_min_index, 1] + np_regroup[chi_min_index + 1, 1]) * (np_regroup[chi_min_index, 2] + np_regroup[chi_min_index + 1, 2]))
            # 删除替换前的卡方值
            chi_table = np.delete(chi_table, chi_min_index + 1, axis=0)
    #print('已完成卡方分箱核心操作，正在保存结果')

    #把结果保存成一个数据框
    result_data = pd.DataFrame()  # 创建一个保存结果的数据框
    result_data['variable'] = [variable] * np_regroup.shape[0]  # 结果表第一列：变量名
    list_temp = []
    for i in np.arange(np_regroup.shape[0]):
        if i == 0:
            x = '0' + ',' + str(np_regroup[i, 0])
        elif i == np_regroup.shape[0] - 1:
            x = str(np_regroup[i - 1, 0]) + '+'
        else:
            x = str(np_regroup[i - 1, 0]) + ',' + str(np_regroup[i, 0])
        list_temp.append(x)
    result_data['interval'] = list_temp  #结果表第二列：区间
    result_data['flag_0'] = np_regroup[:, 2]  # 结果表第三列：负样本数目
    result_data['flag_1'] = np_regroup[:, 1]  # 结果表第四列：正样本数目

    return result_data
   
   
   result_data = ChiMerge(df=data,variable="AGE",flag="target",confidenceVal=3.841,bin=10,sample=None)

bins = [] #卡方的区间值
bins.append(-float('inf'))
for i in range(result_data["interval"].shape[0]-1):
    
    St = result_data["interval"][i].split(",")
    bins.append(float(St[1]))

bins.append(float('inf'))
bins

5.分箱之后

分箱TIPS

基于负样本占比差异最大化的分箱原则，箱的总数最好控制在5箱之内，可以适当调整，最好不要超过10箱，每一箱之间的负样本占比差值尽可能大。每一个箱的样本量不能小于整体样本的5%，原则上不能太小。

特征筛选

原则上来说，我觉得分箱和WOE都是特征编码的过程，在编码之后。可以用IV值，KS,PSI进行特征评估和筛选。

特征编码

参考资料：[1]: https://www.cnblogs.com/wqbin/p/10547167.html

Related Posts

rss facebook twitter github youtube mail spotify lastfm instagram linkedin google google-plus pinterest medium vimeo stackoverflow reddit quora quora