[智能风控]WOE编码
- 4 mins待补!数据不全,先写WOE编码
WOE编码
WOE的全称是“Weight of Evidence”,即证据权重,WOE是对原始自变量的一种编码形式。定义为:
其中,$p_{y_{i}}$是这个分组中响应客户占样本汇总所有响应用户的比例,$p_{n_{i}}$是这个分组中未响应客户占样本所有未响应客户的比例。
WOE可以理解为“当前分组中响应客户占样本所有响应用户的比例”和“当前分组中没有响应的客户占样本中所有没有响应的比例”的差异性。WOE越大,这种差异越大,这个分组里的样本响应的可能性就越大,WOE越小,差异越小,这个分组里的样本响应的可能性就越小。
理解一下WOE,会发现,WOE其实描述了变量当前这个分组,对判断个体是否会响应(或者说属于哪个类)所起到影响方向和大小,当WOE为正时,变量当前取值对判断个体是否会响应起到的正向的影响,当WOE为负时,起到了负向影响。而WOE值的大小,则是这个影响的大小的体现
字符型WOE编码
IV值
IV值用途
IV的全称是Information Value,中文意思是信息价值,或者信息量。
我们在用逻辑回归、决策树等模型方法构建分类模型时,经常需要对自变量进行筛选。比如我们有200个候选自变量,通常情况下,不会直接把200个变量直接放到模型中去进行拟合训练,而是会用一些方法,从这200个自变量中挑选一些出来,放进模型,形成入模变量列表。那么我们怎么去挑选入模变量呢?
挑选入模变量过程是个比较复杂的过程,需要考虑的因素很多,比如:变量的预测能力,变量之间的相关性,变量的简单性(容易生成和使用),变量的强壮性(不容易被绕过),变量在业务上的可解释性(被挑战时可以解释的通)等等。但是,其中最主要和最直接的衡量标准是变量的预测能力。
“变量的预测能力”这个说法很笼统,很主观,非量化,在筛选变量的时候我们总不能说:“我觉得这个变量预测能力很强,所以他要进入模型”吧?我们需要一些具体的量化指标来衡量每自变量的预测能力,并根据这些量化指标的大小,来确定哪些变量进入模型。IV就是这样一种指标,他可以用来衡量自变量的预测能力。类似的指标还有信息增益、基尼系数等等。
预测的直观理解
从直观逻辑上大体可以这样理解“用IV去衡量变量预测能力”这件事情:我们假设在一个分类问题中,目标变量的类别有两类:Y1,Y2。对于一个待预测的个体A,要判断A属于Y1还是Y2,我们是需要一定的信息的,假设这个信息总量是I,而这些所需要的信息,就蕴含在所有的自变量C1,C2,C3,……,Cn中,那么,对于其中的一个变量Ci来说,其蕴含的信息越多,那么它对于判断A属于Y1还是Y2的贡献就越大,Ci的信息价值就越大,Ci的IV就越大,它就越应该进入到入模变量列表中
IV值的计算
IV值的计算依赖于WOE,IV是一个很好的衡量自变量对目标变量影响程度的指标。
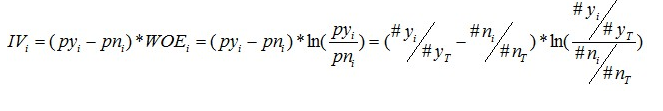
IV值的范围是$[0,+\infty)$,当前分组中只包含响应客户或者未响应客户时,$IV= +\infty$

TIPS
- IV值只用于粗粒度的筛选
- 为什么用IV而不是直接用WOE?
- 当我们衡量一个变量的预测能力时,我们所使用的指标值不应该是负数
- IV在WOE的前面乘以了一个系数,而这个系数很好的考虑了这个分组中样本占整体样本的比例,比例越低,这个分组对变量整体预测能力的贡献越低。相反,如果直接用WOE的绝对值加和,会得到一个很高的指标,这是不合理的
- IV其实有一个缺点,就是不能自动处理变量的分组中出现响应比例为0或100%的情况。
- 如果可能,直接把这个分组做成一个规则,作为模型的前置条件或补充条件;
- 重新对变量进行离散化或分组,使每个分组的响应比例都不为0且不为100%,尤其是当一个分组个体数很小时(比如小于100个),强烈建议这样做,因为本身把一个分组个体数弄得很小就不是太合理。
- 如果上面两种方法都无法使用,建议人工把该分组的响应数和非响应的数量进行一定的调整。如果响应数原本为0,可以人工调整响应数为1,如果非响应数原本为0,可以人工调整非响应数为1.
以UCI credit AGE字段模拟计算IV和WOE
#!/usr/bin/env python3
# encoding: utf-8
'''
@author: ethan
@license: (C) Copyright 2017-2019, Personal exclusive right.
@contact: fantasticethan999@gmail.com
@application:
@file: charWoe.py
@time: 2020/4/12 下午3:13
@desc:
'''
import math
import pandas as pd
from sklearn.model_selection import train_test_split
class datasets(object):
def __init__(self):
data_type = {'AGE':str,'target':str}
self.data = pd.read_csv('/home/amax/workspace/ethan_workspace/risk'
'/projects/In_risk/data/UCI_Credit_Card.csv', dtype=data_type)
self.dev, self.test = train_test_split(self.data, test_size=0.2)
self.val,self.off = train_test_split(self.test, test_size=0.5)
def gets(self,type,name):
if type == "dev":
return self.dev
elif type == "val":
return self.val
elif type == "off":
return self.off
class charWoe(object):
def __init__(self,datasets,dep,weight,vars):
"""
数据集:param datasets: object,has function gets("xx","")
标签:param dep: string
样本权重:param weight: list
参与建模特征名:param vars: list
"""
self.datasets = datasets
self.devf = datasets.gets("dev","")
self.valf = datasets.gets("val","")
self.offf = datasets.gets("off","")
self.dep = dep
self.weight = weight
self.vars = vars
self.nrows,self.ncols = self.devf.shape
def char_woe(self):
# 得到每一类样本的个数,且加入平滑项使得bad和good都不为0
dic = dict(self.devf.groupby([self.dep]).size())
good = dic.get("0", 0) + 1e-10
bad = dic.get("1", 0) + 1e-10
# 对每一个特征进行遍历。
for col in self.vars:
# 得到每一个特征值对应的样本数。
data = dict(self.devf[[col, self.dep]].groupby(
[col, self.dep]).size())
'''
当前特征取值超过100个的时候,跳过当前取值。
因为取值过多时,WOE分箱的效率较低,建议对特征进行截断。
出现频率过低的特征值统一赋值,放入同一箱内。
'''
if len(data) > 120:
print(col, "contains too many different values...")
continue
# 打印取值个数
print(col, len(data))
dic = dict()
# k是特征名和特征取值的组合,v是样本数
for (k, v) in data.items():
# value为特征名,dp为特征取值
value, dp = k
# 如果找不到key设置为一个空字典
dic.setdefault(value, {})
# 字典中嵌套字典
dic[value][str(dp)] = v
for (k, v) in dic.items():
dic[k] = {str(int(k1)): v1 for (k1, v1) in v.items()}
dic[k]["cnt"] = sum(v.values())
# print(v.get("1"))
bad_rate = round(v.get("1", 0) / dic[k]["cnt"], 5)
dic[k]["bad_rate"] = bad_rate
# 利用定义的函数进行合并。
dic = self.combine_box_char(dic)
# 对每个特征计算WOE值和IV值
IV = 0
for (k, v) in dic.items():
a = v.get("0", 1) / good + 1e-10
b = v.get("1", 1) / bad + 1e-10
dic[k]["Good"] = v.get("0", 0)
dic[k]["Bad"] = v.get("1", 0)
dic[k]["woe"] = round(math.log(a / b), 5)
dic[k]["IV"] = (a-b)*dic[k]["woe"]
IV = IV + dic[k]["IV"]
'''
按照分箱后的点进行分割,
计算得到每一个特征值的WOE值,
将原始特征名加上'_woe'后缀,并赋予WOE值。
'''
for (klis, v) in dic.items():
for k in klis.split(","):
# 训练集进行替换
self.devf.loc[self.devf[col] == k,
"%s_woe" % col] = v["woe"]
# 测试集进行替换
if not isinstance(self.valf, str):
self.valf.loc[self.valf[col] == k,
"%s_woe" % col] = v["woe"]
# 跨时间验证集进行替换
if not isinstance(self.offf, str):
self.offf.loc[self.offf[col] == k,
"%s_woe" % col] = v["woe"]
# 返回新的字典,其中包含三个数据集。
return {"dev": self.devf, "val": self.valf, "off": self.offf}
def combine_box_char(self, dic):
'''
实施两种分箱策略。
1.不同箱之间负样本占比差异最大化。
2.每一箱的样本量不能过少。
'''
# 首先合并至10箱以内。按照每一箱负样本占比差异最大化原则进行分箱。
while len(dic) >= 10:
# k是特征值,v["bad_rate"]是特征值对应的负样本占比
bad_rate_dic = {k: v["bad_rate"]
for (k, v) in dic.items()}
# 按照负样本占比排序。因为离散型变量 是无序的,
# 可以直接写成负样本占比递增的形式。
bad_rate_sorted = sorted(bad_rate_dic.items(),
key=lambda x: x[1])
# 计算每两箱之间的负样本占比差值。
# 准备将差值最小的两箱进行合并。
bad_rate = [bad_rate_sorted[i + 1][1] -
bad_rate_sorted[i][1] for i in
range(len(bad_rate_sorted) - 1)]
min_rate_index = bad_rate.index(min(bad_rate))
# k1和k2是差值最小的两箱的key.
k1, k2 = bad_rate_sorted[min_rate_index][0], \
bad_rate_sorted[min_rate_index + 1][0]
# 得到重新划分后的字典,箱的个数比之前少一。
dic["%s,%s" % (k1, k2)] = dict()
dic["%s,%s" % (k1, k2)]["0"] = dic[k1].get("0", 0) \
+ dic[k2].get("0", 0)
dic["%s,%s" % (k1, k2)]["1"] = dic[k1].get("1", 0) \
+ dic[k2].get("1", 0)
dic["%s,%s" % (k1, k2)]["cnt"] = dic[k1]["cnt"] \
+ dic[k2]["cnt"]
dic["%s,%s" % (k1, k2)]["bad_rate"] = round(
dic["%s,%s" % (k1, k2)]["1"] /
dic["%s,%s" % (k1, k2)]["cnt"], 5)
# 删除旧的key。
del dic[k1], dic[k2]
'''
结束循环后,箱的个数应该少于10。
下面实施第二种分箱策略。
将样本数量少的箱合并至其他箱中,以保证每一箱的样本数量不要太少。
'''
# 记录当前样本最少的箱的个数。
min_cnt = min([v["cnt"] for v in dic.values()])
# 当样本数量小于总样本的5%或者总箱的个数大于5的时候,对箱进行合并
while min_cnt < self.nrows * 0.05 and len(dic) > 5:
min_key = [k for (k, v) in dic.items()
if v["cnt"] == min_cnt][0]
bad_rate_dic = {k: v["bad_rate"]
for (k, v) in dic.items()}
bad_rate_sorted = sorted(bad_rate_dic.items(),
key=lambda x: x[1])
keys = [k[0] for k in bad_rate_sorted]
min_index = keys.index(min_key)
'''''
同样想保持合并后箱之间的负样本占比差异最大化。
由于箱的位置不同,按照三种不同情况进行分类讨论。
'''
# 如果是第一箱,和第二项合并
if min_index == 0:
k1, k2 = keys[:2]
# 如果是最后一箱,和倒数第二箱合并
elif min_index == len(dic) - 1:
k1, k2 = keys[-2:]
# 如果是中间箱,和bad_rate值相差最小的箱合并
else:
bef_bad_rate = dic[min_key]["bad_rate"] \
- dic[keys[min_index - 1]]["bad_rate"]
aft_bad_rate = dic[keys[min_index + 1]]["bad_rate"] - dic[min_key]["bad_rate"]
if bef_bad_rate < aft_bad_rate:
k1, k2 = keys[min_index - 1], min_key
else:
k1, k2 = min_key, keys[min_index + 1]
# 得到重新划分后的字典,箱的个数比之前少一。
dic["%s,%s" % (k1, k2)] = dict()
dic["%s,%s" % (k1, k2)]["0"] = dic[k1].get("0", 0) \
+ dic[k2].get("0", 0)
dic["%s,%s" % (k1, k2)]["1"] = dic[k1].get("1", 0) \
+ dic[k2].get("1", 0)
dic["%s,%s" % (k1, k2)]["cnt"] = dic[k1]["cnt"] \
+ dic[k2]["cnt"]
dic["%s,%s" % (k1, k2)]["bad_rate"] = round(
dic["%s,%s" % (k1, k2)]["1"] /
dic["%s,%s" % (k1, k2)]["cnt"], 5)
# 删除旧的key。
del dic[k1], dic[k2]
# 当前最小的箱的样本个数
min_cnt = min([v["cnt"] for v in dic.values()])
return dic
dataset = datasets()
char_woe = charWoe(datasets=dataset,
dep='target',
weight = [],
vars=['AGE'])
char_woe.char_woe()